Lesson 14: Continuous Random Variables India Dictionary

The most formal, axiomatic definition of a random variable involves measure principle. Continuous random variables are outlined when it comes to units of numbers, together with capabilities that map such sets to possibilities. Random variables are used in all types of economic and financial decision making to carry out random experiments. Statistical tools and probability distribution are used to determine the probable outcomes in a given scenario, and thus facilitate decision making. The above table is known as the probability mass function or PMF in statistics. Let’s take another example where we are rolling two dice at the same time and our event is to calculate the sum of two dies.

A continuous random variable is that which has infinite possible values. A variable like this is defined over a range of values rather than a single value. The weight of a person is an example of a continuous random variable. A probability density function is used to describe a continuous random variable because the probability that it will take on an exact value is zero. The Random variable is a numerical description of the outcome of a statistical experiment.

In this short monograph, I proposed a probability-based distance measure for computing dissimilarity between observations for discrete variables thought to be randomly distributed. As their probabilities are derived empirically, there is no underlying assumption on their distribution. We counted the number of tails and the number of ears with earrings. In this course we shall focus on discrete random variables only. If X is discrete random variable with probability mass function p.

Thus the probability function is given as follows. Random variables are also helpful in enabling probabilities to be allocated to a set of potential values. In the discrete case the weights are given by the probability mass perform, and in the continuous case the weights are given by the likelihood density operate.

There are two forms of data, discrete and continuous. A discrete random variable can have an exact value, whereas the value of a continuous random variable will lie within a specific range. A probability distribution and probability mass functions can both be used to define a discrete probability distribution. A continuous probability distribution is described using a probability distribution function and a probability density function.

Continuous Random Variable

An example of a continuous variable is temperature as we can have decimals while measuring temperature and it can take on any value in an interval. In nature, almost all the variables present are continuous until the size reaches a quantum level. Therefore, at a macroscopic level, the mass, temperature, energy, speed, length, and so on are all examples of continuous variables. Assuming that the sample is representative of the population, we can calculate the empirical probability of each class for each variable.

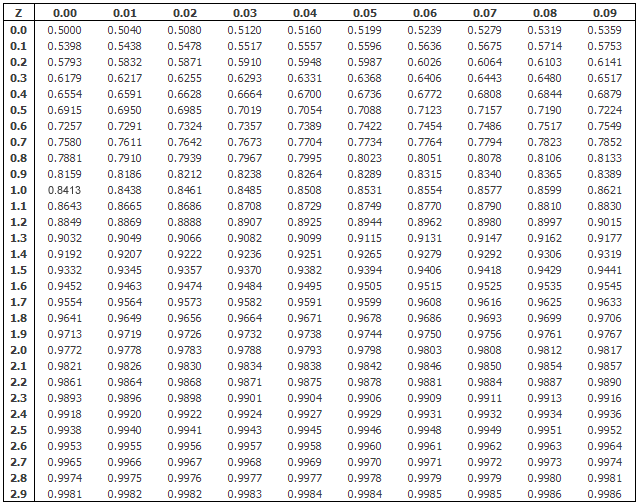
We can, at best, say what the chance is of a set of states. Normal distributionA family of continuous probability distributions such that the probability density function is the normal function. Even though they «look like» discrete variables, these are still continuous random variables, and we will in most cases treat them as such. If X is continuous random variable with probability density function f X .

Combining different random variables

A variable which can assume finite number of possible values or an infinite sequence of countable real numbers is called a discrete random variable. A random variable has a chance distribution that represents the probability that any of the attainable values would occur. Let’s say that the random variable, Z, is the quantity on the top face of a die when it’s rolled once. The probability of each of those values is 1/6 as they are all equally more likely to be the value of Z. Risk analysts assign random variables to threat fashions after they need to estimate the probability of an antagonistic event occurring. These variables are offered utilizing instruments corresponding to situation and sensitivity evaluation tables which threat managers use to make choices concerning danger mitigation.

For instance, the letter X may be designated to represent the sum of the ensuing numbers after three dice are rolled. In this case, X might be 3 (1 + 1+ 1), 18 (6 + 6 + 6), or someplace between 3 and 18, since the highest number of a die is 6 and the bottom number is 1. ‘ Let 0, elsewhere be the joint probability density function of X and Y. Find the moment generating function of this distribution. Age can every so often be considered as continuous or discrete variable. For example, we usually depict age as only a number of years, but occasionally we discuss a polar bear being to live beyond 18-20years old.

Grab Discrete Variable to Grasp Continuous Variable

Note that the method doesn’t guarantee a differentiable score. Even observations with which we get precisely the same can differ from one another. However, observations with very different scores would inevitably be different observations.

A random variable is a numerical description of the outcome of a statistical experiment. The objective is then to find out the likelihood of the outcomes of a perform relying on that state. When it involves conditioning, we would have to introduce all variables we’d need to condition on, by their distribution in a huge joint probability area of distributions. In chance and statistics, random variables are used to quantify outcomes of a random incidence, and therefore, can take on many values. Random variables are required to be measurable and are typically real numbers.

The formulas for computing the expected values of discrete and steady random variables are given by equations 2 and three, respectively. A random variable is a variable whose worth is unknown or a function that assigns values to each of an experiment’s outcomes. Many candidates did not attempt this question and many others were clearly not familiar with this topic. On the other hand, most of the candidates who were familiar with continuous random variables and knew how to start the questions were successful and scored well in parts and . The most common errors were in the integral of \(\), having the limits from \( – \infty \) to 1, confusion over powers and signs (‘-’ sometimes just disappeared).

What is a random variable in statistics?

When evaluated at a point, \(x\), it takes values less than or equal to \(x\). Hence, we always talk of the probability of a continuous random variable lying in an interval. The Distribution Function for a random variable describes how the probabilities are distributed over the values of the random variable. For a random variable X the probability distribution function is defined by a probability mass function, denoted as f. This function provides the probability for each value of the random variable X. The formal mathematical treatment of random variables is a topic in probability principle.

• However, it could not be any number between 0 and plus infinity.
• Assume salaries are normally distributed with a standard deviation of $4,500.
• What differentiates random variables from other variables is that the values for these variables are determined by a random trial, random sample, or simulation.
• A ‘random variable’ means a numerical description of the outcome of a statistical experiment.
• Bernoulli distribution is a discrete probability distribution.

Students must have many questions with respect to Random Variables and its Probability Distributions. Here are a few commonly asked questions and answers. The modulus \((|X|)\) is also a random variable for any random variable \(\mathrm\). For any constants \(\mathrm\) and \(\mathrm, \mathrm x+\mathrm y\) is also a random variable.

Probability Distribution: Applications

A random variable has a chance distribution, which specifies the likelihood of Borel subsets of its vary. Of course, what these subgraph counts are is a set of random variables, and the purpose is that you could analyse their distributions. I do not think you would do this sort of analysis without implicitly using the idea of a random variable, and you then might as well make it explicit.

For example, in a random experiment of a selection of one ball each from two packs containing numbered balls from 1 to 20. Find the probability that in tossing 4 coins one will get either all heads or all tails for the third time on the seventh toss. A small town has one fire engine and one ambulance available for emergencies. The probability that the fire engine is available when a continuous random variable may assume needed is 0.98, and the probability that the ambulance is available when called is 0.92. In the event of an injury resulting from a burning building, find the probability that both the ambulance and the fire engine will be available, assuming they operate independently. Scatter plotA type of display using Cartesian coordinates to display values for two variables for a set of data.

The latter property is more critical when deciding which cluster an observation belongs to. Find the value, correct to two decimal places, at which the mean should be set so that only \(4\)% of the bags are rejected. Find the probability, correct to four significant figures, that a given component fails within six months. Find the value of k , giving a reason for your answer.